那些让你崩溃的编程题02
各位小盆友们,大家好!欢迎继续收看 “那些让你崩溃的编程题” 系列。
ps:这是这个系列的第二期帖子。
这时候,看了标题的小盆友就会问了:“哎呦哎呦,一个模板题,为什么能让你崩溃呢?”
别急,看完下面的内容,你就知道哎呦有多菜哎呦为什么会崩溃了~
点击我返回帖子索引
P3379 【模板】最近公共祖先(LCA)
题目描述
题目传送门
如题,给定一棵有根多叉树,请求出指定两个点直接最近的公共祖先。
输入格式
第一行包含三个正整数 N,M,S,分别表示树的结点个数、询问的个数和树根结点的序号。
接下来 N-1 行每行包含两个正整数 x,y,表示 x 结点和 y 结点之间有一条直接连接的边(数据保证可以构成树)。
接下来 M 行每行包含两个正整数 a,b,表示询问 a 结点和 b 结点的最近公共祖先。
输出格式
输出包含 M 行,每行包含一个正整数,依次为每一个询问的结果。
输入输出样例
输入 #1
5 5 4
3 1
2 4
5 1
1 4
2 4
3 2
3 5
1 2
4 5
输出 #1
4
4
1
4
4
说明/提示
对于 30% 的数据,N≤10,M≤10。
对于 70% 的数据,N≤10000,M≤10000。
对于 100% 的数据,1≤N,M≤500000,1≤x,y,a,b≤N,不保证 a ≠ b。
样例说明:
该树结构如下:
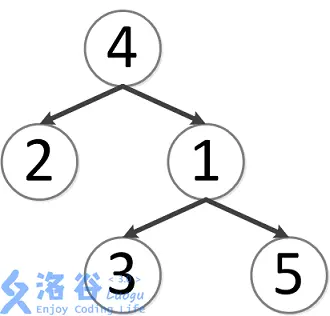
第一次询问:2,4 的最近公共祖先,故为 4。
第二次询问:3,2 的最近公共祖先,故为 4。
第三次询问:3,5 的最近公共祖先,故为 1。
第四次询问:1,2 的最近公共祖先,故为 4。
第五次询问:4,5 的最近公共祖先,故为 4。
故输出依次为 4,4,1,4,4。
题目解析+做题过程
其实这道题真的就是一个模板题,适合像哎呦这样的初学者学习。
在给大家讲题之前,先给大家科普一下几个求最近公共祖先的方法:
·1.倍增法,倍增法的本质是通过已知的一段内容,将该内容求解的范围扩大一倍,进而求解整个问题,从而提升程序效率。(从洛谷题解上抄来的),原文链接
·2.树剖法,但是我不会……
·3.欧拉序,依旧没听说过……
然后,又会有小盆友说了:区区一个最近公共祖先,我用一个暴力不就算出来了?
很遗憾,原题底下有一行这样的文字:应要求加了两组数据卡掉了暴力跳……
这时候,双会有小盆友说了:哎呦哎呦,我没学过最近公共祖先,到底是什么意思啊?
别急,接下来就用几个图来解释一下求最近公共祖先的方法:
所谓最近公共祖先,就是指在一棵树上(如果有人不知道什么是树,那就可以提前走了)选择两个点 u 和 v,
同时是u和v的祖先的所有节点中,深度最大(离 u、v 在树上的距离最近)的那个节点:
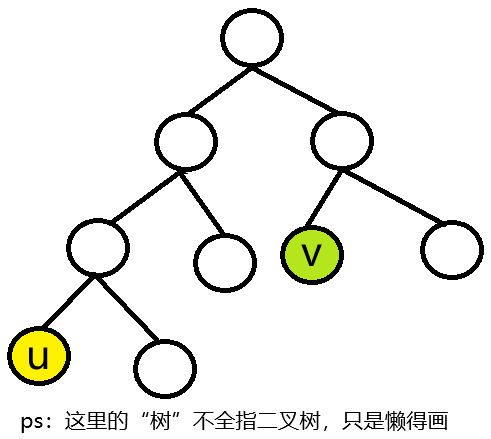
那么,我们立刻就能想到一种暴力的做法:先让位置更低的那个点往上跳到和另一个点相同深度的位置(这里假设 u 点),再让 u 点和 v 点一起每次往上跳一格,最后相遇的那个点就是他们的最近公共祖先,如图:
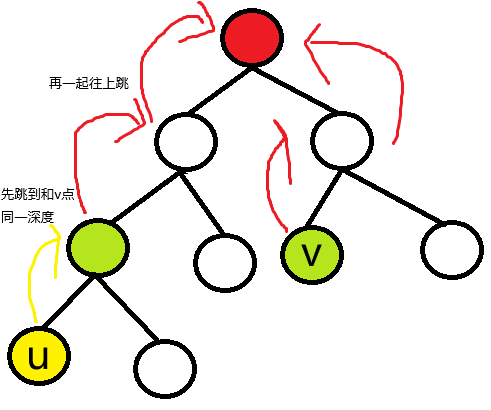
(这绝对是到目前为止图片最多的一期帖子了……)
但是,这样做的时间复杂度为 O(n),对于本题的数据来说还是太慢了,所以,我们还需要在这个方法的基础上进行优化。
试想一下,假设我们一步网上跳 2 格,是不是就能效率翻倍了呢?
如果这样可行的话,我们还可以选择一次往上跳 4 格,8 格,16 格……
但是,照着这种跳法,很可能就会跳过头,从而避开正确答案。所以,我们可以假设需要跳的步数为 k,把 k 分解成几个 2 的不同幂次的形式,再跳上去。例如,假设 k=13,13=8+4+1,只需要跳 3 步就可以让两个点齐平。下图还有一个 k=7 的例子,方便大家理解:
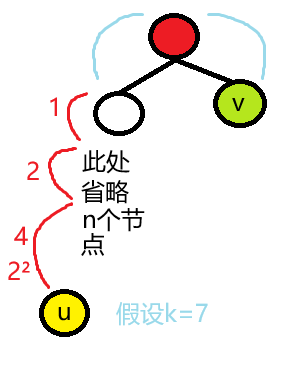
接着,我们就可以开始贴脸开大,用 dp[u][k] 来表示从节点 u 向上跳 2 的 k 次方后所到达的节点的编号(如果越界,就设为 0)。
在本题中,数据范围最大可以到达 500000,而 2 的 20 次方为 1048576,可以覆盖所有数据,所以我们就可以初始化数组为:
//注意本题要建双向边,不然会挂,别问我怎么知道的我就是知道
int head[500010],nxt[1000010],to[1000010],dp[1000010][23],dep[500010];
//这里之所以写23纯是因为想保险一点
好吧,我承认,光是在这一部分就让我卡了0.5小时……
接着,我们就要开始初始化两个东西:一个用来记录各个节点深度,另一个就是刚刚说的dp数组。
(记录深度有利于后面我们对齐 u 和 v 两个节点的深度)。
这里,哎呦选择用dfs深搜来记录两个数组,以下是部分代码:
//相信有能力看到这里的小盆友都已经了解了链式前向星了,就不解释了
void dfs(int x,int y){
dp[x][0] = y; //x的父节点是y,所以可以跳1步到达
dep[x] = dep[y] + 1; //深度数组初始化
//遍历x的所有子节点
for(int i = head[x];i != -1;i = nxt[i]){
int v = to[i];
if(v != y) dfs(v,x); //递归初始化节点v
}
}
然后,在写最重要的 LCA 代码前,还需要对 dp 数组进行初始化,我们可以用循环枚举往上跳 2 的多少次方,再用一个循环枚举节点。
比如,我们站在节点 i 上,要让节点 i 跳 2 的 step 次方步,等价于:
- 先让 i 跳 2 的 step-1 次方步,到达节点
A=dp[i][step-1]; - 再让节点 A 跳 2 的 step-1 次方步,到达节点
dp[i][step]。
好了,做完了前面的这一切,我们就可以正式开始写 LCA 代码了。
由于我们刚刚假设 u 的深度比 v 深,要让 u 跳上来和 v 处于同一深度,所以我们可以在一开始先用一个判断处理一下 v 比 u 深的情况:
if(dep[u] < dep[v]) swap(u,v);
然后,我们就可以开始让 u 往上跳。我们先从最大的 2 的 20 次方开始尝试(为了保险起见哎呦这里写到了 22 次方),只要不跳过头就继续跳,直到深度相同为止。
for(int i = 22;i >= 0;i--){
if(dep[dp[u][i]] >= dep[u]) u = f[u][i]; //不跳过头就跳
}
这个循环过后,两个节点就处于同一深度了。但是这里还有一种情况:如果它们对齐后处于同一个点上,说明他们的最近公共祖先就是同一个,直接特判输出;如果不是,我们就可以进行第二步:让他们同步向上跳,直到相遇为止。这部分的代码和刚刚的很相似,就不展示了。
好了,现在整个题是讲完了,那么,哎呦到底是哪里崩溃了呢?请看图片:
The first try: 被自己调试用的代码送走

The second try: 数组越界

The third try: 被无向图的双向边单杀
The fourth try: ……
……
好吧,这期帖子就到这里,哎呦先去继续刷题了,我们下一篇帖子见!
对了,总有人问我为啥不放完整代码,因为……怕有人看到了说我菜
帖子信息
最新更新时间:2026年1月31日22时30分